Na jó, a címadással csaltam egy kicsit: egyrészt az egyik legerősebb ma ismert és civil használatra megengedett titkosítási eljárásról fogok írni, másrészt a számításelméleti részletekbe egyáltalán nem megyek bele.
A PGP vagy annak egy klónja, megbízható becslések szerint az egész világon a titkosítást alkalmazó kütyük - legyen szó mainframe szerverről vagy filléres mobilról - közt legtöbb helyen alkalmazott titkosítási eljárás. A PGP valójában két titkosítási eljárás, egy asszimmetrikus és valamelyik szimmetrikus módszer alkalmazásaként működik.
 Az asszimmetrikus titkosítás gyakorlatilag minden esetben az RSA módszeren alapul, aminek a működését a következő módon szemléltetném, ráadásul már-már tankönyvi nevekkel: Alice szeretne üzenetet küldeni Bobnak, viszont abban az esetben, ha Alice az üzenetet titkosítja, akkor a titkosításhoz szükséges kulcsot is el kellene juttatnia Bobnak, hogy Bob ugyanazzal a kulccsal az üzenetet vissza tudja fejteni. Abban az esetben, ha a titkosításhoz szükséges kulcsot közben elkapják a titkosított üzenettel együtt, a titkosítás semmit sem ér, hiszen vissza tudja fejteni az is, aki elkapta. Ezzel szemben az asszimmetrikus titkosításnál Alice és Bob egyaránt rendelkezik egy kulcspárral: mindkettőjüknek van egy saját, privát kulcsa, amit csak ő ismer és egy publikus kulcsa, amit bárki ismerhet és ismernie is kell, ha titkosított üzenetet szeretne küldeni neki. Ebben az esetben a történet a következő módon néz ki:
Az asszimmetrikus titkosítás gyakorlatilag minden esetben az RSA módszeren alapul, aminek a működését a következő módon szemléltetném, ráadásul már-már tankönyvi nevekkel: Alice szeretne üzenetet küldeni Bobnak, viszont abban az esetben, ha Alice az üzenetet titkosítja, akkor a titkosításhoz szükséges kulcsot is el kellene juttatnia Bobnak, hogy Bob ugyanazzal a kulccsal az üzenetet vissza tudja fejteni. Abban az esetben, ha a titkosításhoz szükséges kulcsot közben elkapják a titkosított üzenettel együtt, a titkosítás semmit sem ér, hiszen vissza tudja fejteni az is, aki elkapta. Ezzel szemben az asszimmetrikus titkosításnál Alice és Bob egyaránt rendelkezik egy kulcspárral: mindkettőjüknek van egy saját, privát kulcsa, amit csak ő ismer és egy publikus kulcsa, amit bárki ismerhet és ismernie is kell, ha titkosított üzenetet szeretne küldeni neki. Ebben az esetben a történet a következő módon néz ki:
1. Alice és Bob odaadják egymásnak a saját publikus kulcsukat [ezt csak egyszer kell megtenniük]
2. Alice titkosított üzenetet küld Bobnak olyan módon, hogy az üzenet titkosításához a saját privát és Bob publikus kulcsát használja, majd elküldi az üzenetet
3. az üzenet megérkezik Bobhoz, majd az üzenet visszafejtését a saját privát kulcsával, valamint Alice publikus kulcsával végzi el
Azaz egyszer sem haladt át a teljes titkosításhoz szükséges kulcs, mégis tudják olvasni az egymásnak küldött üzeneteket, így az 1970-es években a több ezer éves (!!) ún. kulcsmegosztási problémát oldották meg. Hogyan kombinálódik is az asszimmetrikus és szimmetrikus módszer?
A szimmetrikus kulcsú titkosításnál ugyan csak egy kulcs van, ami a titkosítást és a visszafejtést egyaránt végzi, de ez ideális esetben eléggé erős.
Teljes kommunikáció RSA-val titkosítani egyrészt elképesztően számításigényes lenne, másrészt szükségtelen is, ebből adódott az ötlet, hogy a kettőt össze lehetne lőni, így létrehozva egy olyan titkosítási eljárást, ami kellőképpen erős ahhoz, hogy minden ma ismert törési próbálkozásnak ellenálljon. Ennek az ötletnek az alapján valósította meg Phil Zimmermann a PGP-nek nevezett titkosítási eljárást 1991-ben, ami a következőképp működik:
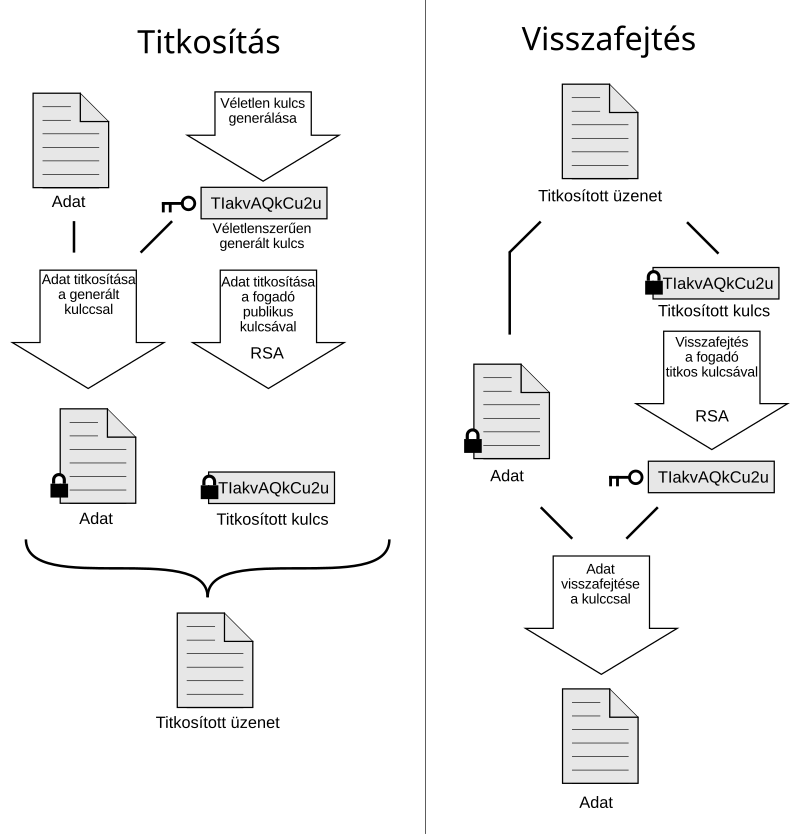
1. Alice tömöríti az üzenetet, hogy a műveleteket kisebb adathalmazon kelljen végrehajtani
2. Alice egy egyszer használatos, akkor generált kulccsal titkosítja az üzenetet egy szimmetrikus módszerrel
3. Alice magához a szimmetrikus titkosításhoz használt kulcsot - amit beágyaz az üzenetbe - titkosítja Bob nyilvános kulcsával, majd elküldi az üzenetet
Bob az üzenet visszafejtésekor a saját privát kulcsával először az asszimmetrikus titkosításhoz használt kulcsot éri el, majd azzal bontja ki a teljes üzenetet.
Kultúrtörténeti érdekesség, hogy az internet hőskorában az, hogy egy egyszerű otthoni számítógéppel olyan erős titkosított üzenetet lehetett létrehozni, amit még a nagy-nagy hárombetűs szervezetek sem tudnak visszafejteni szuperszámítógépekkel, akkora riadalmat keltett, hogy 1993-ban az USA-ban eljárást kezdeményeztek Phil Zimmermann ellen, viszont lévén, hogy nem lehet perelni valakit csak azért, mert túl hatékony algoritmust hozott létre, a vád a fegyverek exportját szabályozó törvény megsértése volt. Végül az eljárást 1996-ban megszüntették vádemelés nélkül, addigra pedig a PGP már úgyis elterjedt az egész világon.
Még középiskolás koromban gondolkoztam azon, hogy ha ennyire egyszerű és ennyire hatékony egy titkosítási eljárás, akkor miért nem megy át minden elképzelhető felhasználói adat két fél közt, azaz például ha emailt vagy SMS-t küldünk valakinek, az eszköz csak betöltené a címtárból a feladó nyilvános kulcsát és a címzett már meg is nyitná az üzenetet a saját privát kulcsával. A teljes magyarázat bőségesen meghaladná ennek a posztnak a kereteit, a legfontosabb indokok mogyoróhéjban az emailezés példáján keresztül: pont a 90-es évek elején robbantak be az ingyenesen elérhető email szolgáltatók, amik döntően webes felületen működtek és a felhasználóik tudatosság szempontjából egész egyszerűen nem voltak érdekeltek abban, hogy az üzeneteik titkosítva legyenek, a szolgáltatóknak pedig nem volt érdekük plusz munkát róni a saját szervereikre, ezen kívül a privát kulcsokat is biztonságosan tárolni kellett volna valahol, ha szempont, hogy a felhasználó a leveleit bárhonnan meg tudja nézni, ne csak azon a gépen, amin a saját privát kulcsa van. Megjegyzem: ebben az időben még pendrive-ok és hasonlók kanyarban sem voltak, amin lehetett volna tárolni és használni a privát kulcsot.
Ma pedig az ingyenes levelezőszolgáltatók leggyakoribb üzleti modellje az, hogy a levelezésért nem kell fizetni, viszont egy algoritmus megvizsgálja a levélben előforduló kifejezéseket, majd annak alapján sebészi pontossággal helyez el targetált hirdetéseket a levél szövege melletti oldallécben. Dollármilliárdos piacról van szó. Ha az üzenet titkosított, természetesen a hirdetés targetálása lehetetlen. A Gmailnek például nyilván veszteséges, de nem tiltja, hogy olyan üzenetek továbbítására használják a felhasználók a fiókjukat, amik teljesen elemezhetetlenek az elemzőmotorjaik számára, ez azonban a felhasználóknak csak nagyon kis részét érinti.
Elméletileg megoldható, hogy egy webes levelezőrendszerben PGP-t alkalmazzanak, ez azonban rendkívüli kockázatot rejt magában, hiszen ha valamilyen módon a privát kulcsokat ellopják, az összes felhasználó titkosított levelezése olvasható lesz, ráadásul új kulcsot kellene mindegyiküknek generálnia. Valójában a publikus levelezőrendszerek közt egyetlen normális kivétel van, a Hushmail, ami a privát kulcsok tárolását saját maga oldja meg, ez a kulcs egyébként le is tölthető.
De mit tegyünk, ha saját magunk akarunk olyan titkosított leveleket küldeni és fogadni, amit aztán tényleg nem olvas se ember, se isten, hacsak nem szerezte meg a privát kulcsunkat? Természetesen több konkrét megvalósítás is van, ezek közül az egyik legelterjedtebb kombót mutatom be, ami működik Windowsban, OSX-en és linuxokon is.
Először is a levelezőszolgáltatónknál engedélyezzük az IMAP4/POP3-letöltést - annyira alap szolgáltatás, hogy ha nem lenne lehetséges, időszerű szolgáltatót váltani - majd telepítsünk fel egy levelezőklienst, például a Thunderbirdöt. Ezt követően szükség lesz egy PGP motorra, amiből többféle is létezik, a legelterjedtebb a Gnu Project által feljesztett GnuPG, ami Windowshoz a http://www.gpg4win.org/ címről, OSX-hez pedig a https://gpgtools.org címről tölthető le, a linux-júzerek meg úgyis tudják. Ezek után a Thunderbirdbe telepítsük az Enigmail addont, ami meg fogja hívni a motort, amikor titkosításra van szükség.
Ha mindez megvan, indítsuk el a GnuPG részeként települt PGA-t [GnuPG Agent] vagy a Kleopatra-t, ahol már gyerekjáték új kulcspárt generálni, kezelni. A kulcsunk mérete lehet 1024, 2048, 3072 és 4096 bites is, viszont erősen ajánlott alapértelmezés szerinti 2048 bites kulcsot generálni, mivel más PGP-szoftverek ezzel garantáltan kompatibilisek, ideértve például mobiltelefonok esetén például Android platformon az APG-t, iPhone-nál használt iPGMailt-t is. Fontos, az is, hogy a kulcs több jellemzője is megváltoztatható, a mérete azonban nem!
Ha a kulcspár készen van, aminek a privát részét egy szerkeszthető jelszó is védi, készítsünk róla másolatot, a publikus kulcsot pedig küldjük át annak, akinek szeretnénk GPG-zet levelet küldeni ill. kérjük el az ő publikus kulcsát. Természetesen azért, hogy mindez egyszerűbb legyen, szerte a neten vannak óriási "GPG-telefonkönyvek", ahol ki lehet keresni más GPG-kulcsát az email címe, neve és egyéb adatok alapján, így a publikus kulcsok betölthetők a saját helyi kulcstárunkba illetve mi is feltölthetjük a sajátunkat. Ha egy nagy GPG-adatbázisba feltöltöttük a publikus kulcsunkat, a többibe már nem szükséges, hiszen ezek szinkronban vannak egymással, Magyarországon ilyen például a http://keys.niif.hu/
Amint mindez kész, írjuk meg a titkosítani kívánt levelet, majd küldéskor üssük be a privát kulcsunkhoz tartozó jelszavunkat, az Enigmail pedig a címzett alapján tudni fogja, hogy kinek a publikus kulcsát kell használnia az üzenet titkosításához a kulcstárunkból és a levelet el is küldtük.
Ami még hatalmas előnye a megoldásnak, hogy ha a levelet digitálisan alá is írtuk, az megmásíthatatlanul bizonyítja, hogy a levelet valóban mi írtuk, akkor, azzal a tartalommal, közben nem írt át benne senki semmit és mivel egy GPG-kulcshoz több email cím is hozzárendelhető, ha az email címünk megváltozik, de a leveleinket továbbra is aláirkáljuk, az igazolja a címzett oldalán, hogy tényleg mi vagyunk csak más címmel, nem pedig valaki a nevünkben akar levelet írni.
A posztban nem tértem ki rá, hogy természetesen minden normális levelezőklienshez hozzá lehet adni olyan kiegészítőt, ami lehetővé teszi a PGP-zést, csak éppen van, amelyikben iszonyatosan fapados módon működik. Ahogy nem tértem ki a kulcspár finomhangolási lehetőségeire sem [érvényességi idő, kulcs értvénytelenítésének lehetősége].
Amit viszont nagyon fontos megjegyeznem, hogy a szimmetrikus- és asszimmetrikus titkosítást természetesen nem csak emailek titkosításánál használják, hanem ez a lelke például az SSL/TSL-titkosításnak is, aminek a nyomát nap, mint nap látunk a böngészőben szinte minden, önmagára valamit is adó webszolgáltatásnál, kis lakatként a böngészőben a címsor elején. Ott az egyszer használatos kulcs ismétcsak nálunk van, de a böngésző belügye, hogy azt hogyan kezeli, míg a publikus kulcs a szervernél, ami éppen kiszolgálja a webhelyet. A titkosítás eléggé világos ok miatt sokkal kisebb, mint 2048 bites kulccsal dolgozik. De a technika egyre több internetes telefonálást vagy chatelést biztosító szolgáltatásban is ott figyel, nem mellékesen nem mindegyikben, amelyikre a gyártó azt mondja, hogy igen. A ütősebb, jóval erősebb hardveres titkosítást alkalmazó pendriveok titkosításának az alapja ugyanez.
Néhány kapcsolódó téma, amibe most szintén nem mentem bele: az alkalmazott asszimmetrikus módszertől függően bizonyos kulcsok csak titkosításra használhatók, digitális aláírásra viszont nem valamint az, hogy a titkosítás szigorúan számításelméleti szempontból feltörhetetlen, nem jelenti azt, hogy a gyakorlatban is az: például, ha az egész véletlenül hibásan van leprogramozva vagy az algoritmusnak az a része, ami a kulcspárok generálásához a dög nagy prímszámokat nem teljesen véletlenül választja ki, így a lehetséges privát kulcsokból sokkal kevesebb állítható elő - amiből nemrég orbitális botrány is lett.
A GPG-ről egyébként Thunderbird-GunPG-specifikusabban egy behatóbb cikket is írtam néhány napja, amit itt találtok meg.
[kollégák figyelmébe: itt ismeretterjesztő cikkről van szó, ennek megfelelően lett megírva, az egyszerűsítések és az érthetőség kedvéért alkalmazott kevésbé precíz megfogalmazás, a PGP és GPG itt-ott szinonimaként való használata az érthetőséget hivatott szolgálni] A magyarázó ábra forrása: Wikipedia.



 Sophos Naked Security
Sophos Naked Security Securelist
Securelist cyber-secret futurist
cyber-secret futurist I'm, the bookworm
I'm, the bookworm Az asszimmetrikus titkosítás gyakorlatilag minden esetben az RSA módszeren alapul, aminek a működését a következő módon szemléltetném, ráadásul már-már tankönyvi nevekkel: Alice szeretne üzenetet küldeni Bobnak, viszont abban az esetben, ha Alice az üzenetet titkosítja, akkor a titkosításhoz szükséges kulcsot is el kellene juttatnia Bobnak, hogy Bob ugyanazzal a kulccsal az üzenetet vissza tudja fejteni. Abban az esetben, ha a titkosításhoz szükséges kulcsot közben elkapják a titkosított üzenettel együtt, a titkosítás semmit sem ér, hiszen vissza tudja fejteni az is, aki elkapta. Ezzel szemben az asszimmetrikus titkosításnál Alice és Bob egyaránt rendelkezik egy kulcspárral: mindkettőjüknek van egy saját, privát kulcsa, amit csak ő ismer és egy publikus kulcsa, amit bárki ismerhet és ismernie is kell, ha titkosított üzenetet szeretne küldeni neki. Ebben az esetben a történet a következő módon néz ki:
Az asszimmetrikus titkosítás gyakorlatilag minden esetben az RSA módszeren alapul, aminek a működését a következő módon szemléltetném, ráadásul már-már tankönyvi nevekkel: Alice szeretne üzenetet küldeni Bobnak, viszont abban az esetben, ha Alice az üzenetet titkosítja, akkor a titkosításhoz szükséges kulcsot is el kellene juttatnia Bobnak, hogy Bob ugyanazzal a kulccsal az üzenetet vissza tudja fejteni. Abban az esetben, ha a titkosításhoz szükséges kulcsot közben elkapják a titkosított üzenettel együtt, a titkosítás semmit sem ér, hiszen vissza tudja fejteni az is, aki elkapta. Ezzel szemben az asszimmetrikus titkosításnál Alice és Bob egyaránt rendelkezik egy kulcspárral: mindkettőjüknek van egy saját, privát kulcsa, amit csak ő ismer és egy publikus kulcsa, amit bárki ismerhet és ismernie is kell, ha titkosított üzenetet szeretne küldeni neki. Ebben az esetben a történet a következő módon néz ki: 

